💐解码与部署

大语言模型是通过文本生成的方式进行工作的。在自回归架构中，模型针对输入内容逐个单词生成输出内容的文本。这个过程一般被称为 解码。

🌸解码策略

大语言模型的生成方式本质上是一个概率采样过程，需要合适的解码策略来生成合适的输出内容。

🌹语言模型解码的背景知识

模型M每次根据当前上下文词元序列𝒖=[𝑢1,𝑢2,··· ,𝑢𝑡]建模下一个词的概率分布𝑃（即公式$O = softmax(W^LY_L)$的输出），然后根据一定的解码策略选择下一个词𝑢′，之后再将𝒖和𝑢′作为新的上下文重复上述步骤，直到生成结束词元或者达到长度上限为止。在这个流程中，解码策略将主要关注如何基于概率分布𝑃选择合适的下一个词𝑢′。自回归的解码策略并不局限于特定架构，常见的编码器-解码器、因果解码器和前缀解码器均可适用。

🌺贪心搜索

目前常见的大语言模型主要是通过语言建模任务进行预训练的。基于这种训练方式，一种直观的解码策略是贪心搜索（Greedy Search）。具体来说，贪心搜索在每个生成步骤中都选择概率最高的词元， 其可以描述为以下形式:

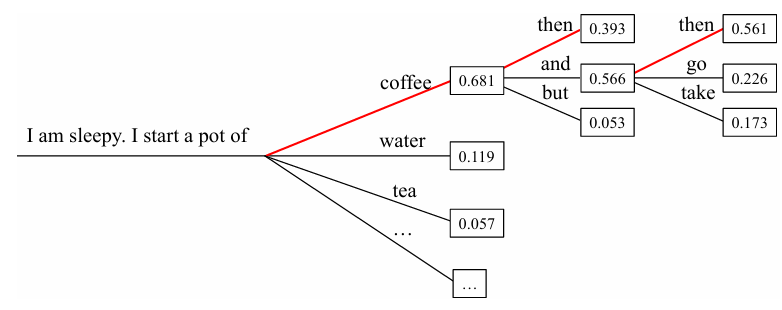
🌻概率采样

该方法根据模型建模的概率分布采样得到下一个词元，旨在增强生成过程中的随机性和结果的多样性：

在图中展示了下一个词元的概率分布，虽然单词“coffee”被选中的概率较高，但基于采样的策略同时也为选择其他单词（如“water”、“tea”等）留有一定的可能性，从而增加了生成文本的多样性和随机性。

🌼贪心搜索的改进

贪心搜索在每个生成步骤中均选择最高概率的词元，这可能会由于忽略在某些步骤中概率不是最高、但是整体生成概率更高的句子而造成局部最优。

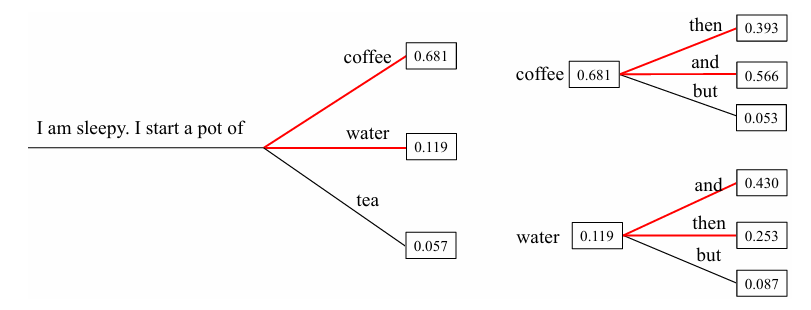
• 束搜索. 在解码过程中，束搜索（BeamSearch）[1]会保留前𝑛个具有最高概率的句子，并最终选取整体概率最高的生成回复。这里的𝑛被称为束大小（Beam Size）。当 𝑛 = 1，束搜索就退化为贪心搜索。如图9.3所示（𝑛=2），第一步保留了概率最高的两个词“coffee” 和 “water” 作为候选；第二步基于 “coffee” 和 “water” 均进行扩展，得到模型在两个上下文内容下的概率分布，最后选择联合概率最高的两个句子 “coffee then” 和 “coffee and” 作为候选。在下面的生成步骤中，将会继续基于这两个候选去进行扩展，每次都选择联合概率最高的两个句子。最后，当两个束的句子均生成结束后，选择整体生成概率最高的候选句子作为最终的输出。在实践中，束的数量通常设定在3到6的范围内，设置过大的束会显著增加运算开销，并可能会导致性能下降。

  

• 长度惩罚. 由于束搜索中需要比较不同长度候选句子的概率，往往需要引入长度惩罚（LengthPenalty）（亦称为长度归一化）技术。如果没有长度惩罚，传统的束搜索会倾向于生成较短的句子，因为每生成一个单词，都会乘以一个小于1的概率，使得句子的生成概率逐渐变小。因此，可以在生成概率的计算中引入长度惩罚，通过将句子概率除以其长度的指数幂𝛼，对于句子概率进行归一化处理，从而鼓励模型生成更长的句子。在实践中，𝛼通常设置为0.6到0.7之间的数值。

• 重复惩罚.为了缓解贪心搜索重复生成的问题，可以使用𝑛-元惩罚（𝑛-gram Penalty）来强制避免生成重复的连续𝑛个词元，实践中𝑛通常设置为3到5之间的整数。进一步地，研究人员还提出了相对“温和”的惩罚机制来降低生成重复词元的概率，而不是“一刀切”地完全避免某些短语的生成，如出现惩罚（Presence Penalty）和频率惩罚（FrequencyPenalty）。具体地，出现惩罚在生成过程中会将已经生成词元的logits减去惩罚项𝛼来降低该词元之后生成的概率。频率惩罚相较于出现惩罚，会记录每个词元生成的数目，然后减去出现次数乘以惩罚项𝛼，因此如果一个词元生成得越多，惩罚也就越大。在实践中，𝛼的取值范围通常在0.1到1之间。这些重复惩罚方法不止适用于贪心搜索，对于随机采样也均适用。

🌷随机采样的改进策略

基于概率采样的方法会在整个词表中选择词元，这可能会导致生成不相干的词元。为了进一步提高生成质量，可以进一步使用一些改进的采样策略，减少具有极低概率词汇对于生成结果的影响。

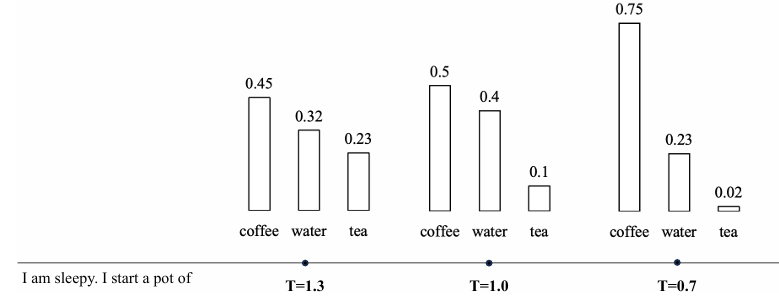
温度采样（TemperatureSampling）. 为了调节采样过程中的随机性，一种有效的方法是调整softmax函数中的温度系数。具体来说，公式5.11中的$l = W^LyL$ 称为logits，调整温度系数后的softmax计算式如下：

其中，$l_{j^′ }$表示每个候选词元的logit，𝑡是温度系数。具体来说，降低温度系数𝑡会使得概率分布更加集中，从而增加了高概率词元的采样可能性，同时降低了低概率词元的采样可能；当温度系数𝑡设置为1时，该公式退化为标准的随机采样方法；而当𝑡趋近于0时，实际上等同于贪心搜索，即总是选择概率最高的词。此外，当𝑡趋近于无穷大时，温度采样会退化为均匀采样。

🌱低资源部署策略

由于大模型的参数量巨大，在解码阶段需要占用大量的显存资源，因而在实际应用中的部署代价非常高。这里介绍一种常用的模型压缩方法，即模型量化（Model Quantization），来减少大模型的显存占用，从而使得能够在资源有限的环境下使用大模型.

🌲量化基础知识

在神经网络压缩中，量化通常是指从浮点数到整数的映射过程[2]，目前比较常用的是8比特整数量化，即INT8量化。针对神经网络模型，通常有两种类型的数据需要进行量化，分别为权重量化（也称为模型参数量化）和激活（值）量化，它们都以浮点数形式进行表示与存储。

🌳量化的数学表述

量化的过程可以表示为一个函数，该函数将连续的输入映射到离散的输出集合。一般来说，这个过程涉及到四舍五入或截断等近似操作。下面介绍一个一般形式的量化函数：

通过上述数学变换，量化算法将浮点数向量𝒙转化为量化值𝒙𝒒。其中，𝑆表示缩放因子，用于确定裁剪范围，𝑍表示零点因子，用于确定对称或非对称量化，𝑅(·) 表示将缩放后的浮点值映射为近似整数的取整操作。一般来说，裁剪范围对于量化性能有很大影响，通常需要根据实际数据分布进行校准，可以通过静态（离线）或动态（运行时）方式。

作为上述变换的逆过程，反量化（Dequantization）对应地从量化值中恢复原始值，该过程首先加上零点因子，然后乘以缩放因子：

进一步，可以定义量化误差是原始值𝒙和恢复值$\tilde{\mathbf{x}}$之间的数值差异：$Δ=∥𝒙−\tilde{\mathbf{x}}∥^2_2$。

🌴量化的策略

基于上述量化函数的定义形式，下面介绍一些对于量化函数常见的分类与实现策略。

• 均匀量化和非均匀量化.根据映射函数的数值范围是否均匀，可以将量化分为两类：均匀量化和非均匀量化。均匀量化是指在量化过程中，量化函数产生的量化值之间的间距是均匀分布的。这种方法通常用于将连续的数据转换为离散的表示，以便在计算机中进行高效处理。与此不同，在非均匀量化方法中，它的量化值不一定均匀分布，可以根据输入数据的分布范围而进行调整。其中，均匀量化方法因其简单和高效的特点而在实际中被广泛使用。

  

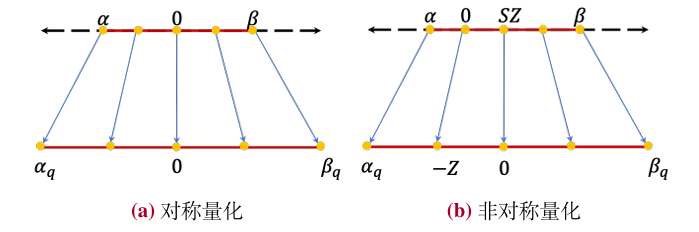
• 对称量化和非对称量化. 根据零点因子𝑍是否为零，均匀量化可以进一步分为两类：对称量化（𝑍=0）和非对称量化（𝑍≠0）。对称量化与非对称量化的一个关键区别在于整数区间零点的映射，对称量化需要确保原始输入数据中的零点（𝑥=0）在量化后仍然对应到整数区间的零点。而非对称量化则不同，根据前面的公式可以看出此时整数区间的零点对应到输入数值的𝑆·𝑍。为了方便讨论，这里以一个常见的8比特量化为例进行介绍。如图9.6(a)和图9.6(b)所示，对称量化将输入数值𝒙通过一个映射公式转换为八比特整数的表示范围内，如果是有符号整数，则该范围可以设置为[−128,127]，适用于𝒙的数值大致分布在零点两侧的情况，如果是无符号整数，则设置为[0,255]，适用于输入数值基本都分布在零点一侧的情况。

• 量化粒度的选择. 量化算法通常针对一个批次的数据进行处理，其中批次的规模大小就反应了量化粒度，可以由算法设计人员进行选择。在神经网络模型中，输入数据和模型权重通常是以张量的形式进行表示与组织的。首先，如果每个张量只定义一组量化参数（即𝑆和𝑍），这称为按张量量化。为了进一步提高量化的精度，可以针对每个张量定义多组量化参数，例如可以为权重矩阵的列维度（也称为“通道”）设置特定的量化参数，称为按通道量化。还有一些研究工作采用了更细粒度的量化方案，对一个通道的数值细分为多个组，即按组的方式进行量化。在神经网络量化中，从按张量到按组，量化粒度越来越小，且使用较小的粒度通常可以提高量化的准确性，有效保持原始模型的性能。但是由于引入了更多的量化参数，在使用时会带来额外的计算开销。相反，按张量量化的粒度较粗，可能会引入较大的误差，但由于在硬件实现上更加简单，也是一种常见的量化粒度选择策略。在实践中，量化粒度需要根据具体任务和模型进行选择，应该采用可以平衡量化准确性以及额外计算开销的合适粒度。

🌵大模型训练后量化方法

基于上述的量化基础知识，本部分将主要介绍大语言模型相关的量化方法。通常来说，模型量化方法可以分为两大类，即量化感知训练（Quantization-Aware Training,QAT）和训练后量化（Post-Training Quantization,PTQ）。从方法的名字可以看出，量化感知训练方法需要更新权重进而完成模型量化，而训练后量化方法则无需更新模型权重。与小型语言模型相比，在为大语言模型设计或选择量化方法时需要侧重关注两个主要因素。首先，大语言模型由大规模神经网络参数组成，在设计量化算法时需要考虑到所需要花费的计算开销。一般来说，训练后量化方法需要更少的算力开销，实践中应用更为广泛。其次，大语言模型中具有不同的数值分布特征（如激活值中存在较大的数值），这使得对于大语言模型进行低比特量化变得非常困难，特别是对于激活值。

🌿权重量化

首先介绍主要面向模型权重的量化方法。其中，主流的权重量化方法通常是基于逐层量化的方法进行设计的，旨在通过最小化逐层的重构损失来优化模型的量化权重，可以刻画为：$\text{argmin}_{\mathbf{W}} | \mathbf{X} \mathbf{W} - \mathbf{X} \mathbf{W} |_2^2$，其中𝑾，𝑾 分别表示原始权重和量化后的权重，𝑿为输入。

为了有效地优化该目标函数，GPTQ[3]的基本想法是在逐层量化的基础上，进一步将权重矩阵按照列维度分组（例如128个列为一组），对一个组内逐列进行量化，每列参数量化后，需要适当调整组内其他未量化的参数，以弥补当前量化造成的精度损失。在具体的实现中，GPTQ还进一步采用了特殊设计的优化方法来加速整个过程，如延迟批次更新、Cholesky重构等。GPTQ可以在3比特或4比特精度下实现对于大语言模型的有效权重量化。

进一步，AWQ[4]发现在逐层和逐组权重量化过程中，对于模型性能重要的权重只占全部参数的一小部分（0.1%∼1%），并且应该更加关注那些与较大激活值维度相对应的关键权重，因为它们对应着更为重要的特征。为了加强对于这部分关键权重的关注，AWQ方法提出引入针对权重的激活感知缩放策略。具体来说，AWQ的优化目标将逐层的重构损失$| \mathbf{X} \mathbf{W} - \mathbf{X} \mathbf{W} |_2^2$修改为：$\left| \left( \text{diag}(\mathbf{s})^{-1} \cdot \mathbf{X} \right) \cdot \mathbf{Q}(\mathbf{W} \cdot \text{diag}(\mathbf{s})) - \mathbf{X} \mathbf{W} \right|_2^2$，其中𝑄 为量化函数。通过引入缩放因子𝒔，AWQ算法可以使得量化方法更为针对性地处理关键权重所对应的权重维度。

☘️模型蒸馏

模型蒸馏（ModelDistillation）的目标是将复杂模型（称为教师模型）包含的知识迁移到简单模型（称为学生模型）中，从而实现复杂模型的压缩。一般来说，通常会使用教师模型的输出来训练学生模型，以此来传递模型知识。以分类问题为例，教师模型和学生模型在中间每一层会输出特征表示（特指神经网络模型），在最后一层会输出针对标签集合的概率分布。模型蒸馏的核心思想是，引入额外的损失函数（称为蒸馏损失函数），训练学生模型的输出尽可能接近教师模型的输出。在实际应用中，蒸馏损失函数通常与分类损失函数（交叉熵损失函数）联合用于训练学生模型。下面首先介绍传统的知识蒸馏方法，再介绍其在大语言模型中的应用。

🍀参考文献

[1]. CARNEGIE-MELLON UNIV PITTSBURGH PA DEPT OF COMPUTER SCIENCE. Speech Understanding Systems. Summary of Results of the Five-Year Research Effort at Carnegie-Mellon University. 1977.

[2]. Amir Gholami et al. “A Survey of Quantization Methods for Efficient Neural Network Inference”. In: arXiv preprint arXiv:2103.13630 (2021).

[3]. EliasFrantaretal.“GPTQ:AccuratePost-TrainingQuantizationforGenerativePre-trained Transformers”. In: arXiv preprint arXiv:2210.17323 (2022).

[4]. Ji Lin et al. “AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration”. In: arXiv preprint arXiv:2306.00978 (2023).